Source Transformation

Source Transformation

In source transformation we have to combine the impedances or simply the circuit. But remember that we must leave the branch which is the required parameter is present on it.

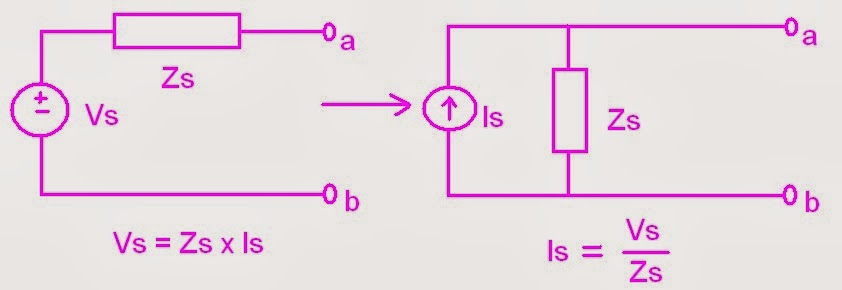
Also in source transformation we will transform the voltage source in series with impedance to a current source in parallel with impedance or vise-versa. The transformation of the source with impedance will only use the ohm's Law

Vs = Zs x Is and Is = Vs / Zs.

Illustration:

           

Example:

                               Vx is our unknown in the given circuit. We have to simplify this circuit to obtain Vx.

* means series

3Ω *  j4 Ω

Z1 =  3 + j4   Ω

4 Ω * -j13 Ω

Z2 = 4 + -j13 Ω

As we can see from the circuit, It has a voltage source with series resistor. We will transform it into a current source with a resistor as what illustration above shows. Using ohm's Law we have;

I = (20∠-90)   /   5   =  -j4 A

                          

5 Ω // (3+ j4 Ω)

Z3 = (3+ j4) (5) /   (3+ j4) + (5)

Z3 = 2.5 + j1.25 Ω

V =   (-j4) x (2.5 + j1.25)

V =  5 - j10 V

                           

   (2.5 + j1.25 Ω) *  (4 + -j13 Ω)

  Z4 =  (2.5 + j1.25) + (4 + -j13) 

  Z4 = 6.5 - j11.75 Ω

By this time, we will apply voltage division.

Vx = ( Zx ) (Vs)    /    (Zx) + (Z)

Vx = ( 10 ) (5 - j10)  /   ( 10 )  (6.5 - j11.75)

Vx =  5. 519 ∠ -27.98 V

I've learned that in solving unknown in Ac circuit, we can also use source transformation. For me this is much easier to use than to the other in simplifying the circuit because it lessen your time making solutions. It gives you many illustrations how the circuit changes while solving the problem. Ohm's Law is the most formula we used in here so it is quiet easy. Source transformation can be use for checking your circuit if you are confused.