Instantaneous and Average Power

__________________________________________________

I've learned that in solving power, there are many different ways and different formula but comes up with the same answer. I also learned that resistor is the resistive load which also absorbs power from the source. This means that most loads in our home are resistive because we are paying bills for the power we consumed.

I've learned that in AC source capacitors are able to store Power and releases power. They are not like resistive loads that absorb power and dissipate power in the form of heat. 

Thevenin's and Norton Theorem

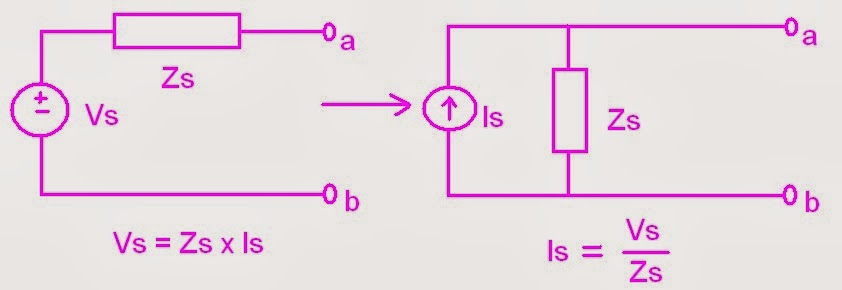
Thevenin's Theorem- states that any network of voltage sources and resistors can be reduced to a single voltage source and a single resistor which are in SERIES with each other.

Example problem;

             In the circuit above we are required to obtain the thevenin's circuit equivalent.

thevenin's circuit equivalent

                           To achieve this goal, on the circuit given above we must acquire Vth and Zth. To do this, in getting Zth we first kill all sources present in the circuit. We have

So let's apply the series-parallel combination.

* -  means series

//  means parallel

j2 Ω * 6 Ω

Z1 = 6 + j2  Ω

Z1// -j4

Z2 = (6+j2)(-j4)   /    (6+j2)+(-j4)

Z2 = 12/5   -  j16/5   Ω

Z2 * 10 Ω

Zth = 62/5 - j16/5 Ω

 next is to solve for Vth. let's use again our 1st circuit.

                 In solving Vth we can apply any analysis that is fit to the circuit. We will use KVL.

75∠ 20 = 6 I + j2 I + (-j4) I

75∠ 20 = I (6  + j2  + (-j4))

I =  11.86∠ 38.43 A

Vth= I x Z (capacitor)

Vth =  11.86∠ 38.43 x  (-j4)

Vth = 47.43∠ -51.565 

What happen to 10  Ω resistor?

Our circuit on the right side is open. one terminal of our resistor is hanged. Therefore there is no current present across this resistor.

our thevenin equivalent circuit is :

                  I've learned that in solving circuit using thevenin's theorem in AC circuit it has the same application as we solve the dc circuits.The difference is the application of complex numbers. 

Source Transformation

Source Transformation

In source transformation we have to combine the impedances or simply the circuit. But remember that we must leave the branch which is the required parameter is present on it.

Also in source transformation we will transform the voltage source in series with impedance to a current source in parallel with impedance or vise-versa. The transformation of the source with impedance will only use the ohm's Law

Vs = Zs x Is and Is = Vs / Zs.

Illustration:

           

Example:

                               Vx is our unknown in the given circuit. We have to simplify this circuit to obtain Vx.

* means series

3Ω *  j4 Ω

Z1 =  3 + j4   Ω

4 Ω * -j13 Ω

Z2 = 4 + -j13 Ω

As we can see from the circuit, It has a voltage source with series resistor. We will transform it into a current source with a resistor as what illustration above shows. Using ohm's Law we have;

I = (20∠-90)   /   5   =  -j4 A

                          

5 Ω // (3+ j4 Ω)

Z3 = (3+ j4) (5) /   (3+ j4) + (5)

Z3 = 2.5 + j1.25 Ω

V =   (-j4) x (2.5 + j1.25)

V =  5 - j10 V

                           

   (2.5 + j1.25 Ω) *  (4 + -j13 Ω)

  Z4 =  (2.5 + j1.25) + (4 + -j13) 

  Z4 = 6.5 - j11.75 Ω

By this time, we will apply voltage division.

Vx = ( Zx ) (Vs)    /    (Zx) + (Z)

Vx = ( 10 ) (5 - j10)  /   ( 10 )  (6.5 - j11.75)

Vx =  5. 519 ∠ -27.98 V

I've learned that in solving unknown in Ac circuit, we can also use source transformation. For me this is much easier to use than to the other in simplifying the circuit because it lessen your time making solutions. It gives you many illustrations how the circuit changes while solving the problem. Ohm's Law is the most formula we used in here so it is quiet easy. Source transformation can be use for checking your circuit if you are confused.