Superposition Theorem

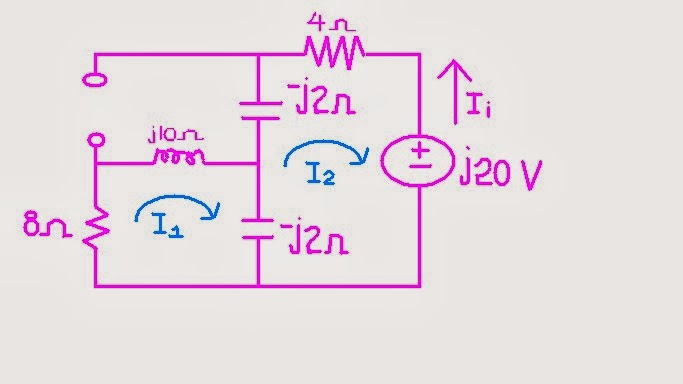
               In our previous discussion we learned that the forced steady-state response of circuits to sinusoidal inputs can be obtain by using phasor where this phasor is in complex form. In this section we will discuss about in the superposition theorem in the form of phasors in knowing current and voltages. 

               The principle of superposition states that the response (a desired current or voltage) in a linear circuit having more than one independent source can be obtained by adding the responses caused by the separate independent sources acting alone.

              The superposition theorem gives a method for finding the currents in the circuit which then enables all the voltage drops to be calculated. The procedure is described below:

-Redraw the circuit for each e.m.f. in turn shorting out the other e.m.f

-Calculate the currents that would flow due to each e.m.f. acting alone

-Finally add the branch currents from each of the circuits (taking into account their direction*) to find the branch currents for the original circuit

-Use these currents to find the voltage drops in the original circuit

Example problem:

             Using super position we have to kill sources across the circuit and leave one voltage source. We have two sources. This means that we have two circuits. We have to solve each of its current at the same branch.

Killing the current source

 Remember that we should leave voltage source, current must be set to zero and the path leaved open.

In the circuit we can now perform the series-parallel to make it simpler.

8  Ω * j10  Ω          (* means series)

Z1 = 8  Ω + j10  Ω

Z1 // -j2  ( below capacitor)               // means parallel

Z2 = (8 + j10 )(-j2)   /    (8 + j10 ) + (-j2)

Z2 = 1/4  -  j 9/4

Z2  *  -j2   (above capacitor)

Z3 =  (1/4  -  j 9/4)  +   -j2

Z3 =  1/4  -  j 17/4

            


  =tis illustration is the a branch contains a multiple of impedance came from different branches after simplifying the circuit.

This circuit we are looking for current of 4Ω so we will use KVL.

(1/4  -  j 17/4) I  +  4 I  = -j20

((1/4  -  j 17/4) +  4 ) I  = -j20

I = 2.353 - j2.353

Since I =  -I1        (negative because of the opposite directions of currents)

I1 =  - 2.353 + j2.353 A

I1 =  3.33 ∠ 135 A    (first current)

Killing the voltage source

                   We have to remember that, it is important to leave the branch that has the required unknown value at ease so that we can easily get its value. (I am talking about the 4 Ω resistor)

In this circuit we can use mesh analysis for better calculations.

I3 =  5 A     --------> equation 1

@ mesh 1

8 I1 + j10 I3 - j10 I3 - j2 I1 + j2 I2 = 0

Since we already have I3, substitute this equation @ mesh 1

I1 (8+j8) + j2 I2 = 50i   ---------> equation 2

@mesh 2

-j2 I2 + - j2 I1 - j2 I2 + j2 I3 + 4 I2 =0

I2 (4-4j) + j2 I1 = -j10 --------> equation 3

Using matrix,

 (8+j8)       j2         = 50i

  j2           (4-4j)     = -j10     

            Δ2 =   (8+j8)(4-4j) + (  j2 )(  j2 )

Δ =  68

We will only solve the I2 in the equation. We don't need I1.

Δ2 =   (8+j8)(-j10 )  -  (50i)(j2 )

Δ2 = 180 - j80

So,

I2= (Δ2  /  Δ)

= (180 - j80)  /   68

= 2.90 ∠ -23.96  A   (second current) 

Our first current is  3.33 ∠ 135 A and second current is 2.90 ∠ -23.96  A. To get the actual value of the required parameter we will add up the two current.

Yields,

Total current I = 3.33 ∠ 135     +      2.90 ∠ -23.96

                   I = 6.116∠144.978 A

_____________________________________________

* Note to add the branch currents while taking into account their direction may actually require one current to be subtracted from another. If both currents are flowing in the same direction you simply add them, but if the currents are flowing in opposite directions you subtract the smaller current from the larger one. The resultant current will flow in the same direction as the larger current.

I've learned that in super position theorem can be apply to AC circuits. And its application is the same way to DC circuits. The difference is, it uses complex number in AC circuit. I learned that this theorem is very useful when the sources are in different frequencies.

I also learned that since source are in different frequencies the impedance must be solved in separate but the same circuit and contains one source (the rest must be set to zero or kill) it is because impedance depends on frequency. With this, each circuit must produce required values of the required parameter.

mesh analysis

mesh analysis

We already have a background in solving circuits using the mesh analysis. We are now ready to put things more complicated using the complex number as what we had tackled previously.

Mesh analysis

Mesh is a loop which does not contain any other loop within it.

                In solving with mesh analysis, our basis is the Kirchhoff's voltage law or (KVL). This will give us a set of equations that we will solve to find the mesh currents. Once we find the mesh currents we can use them to calculate any other currents or voltages. Remember that in using KVL in every mesh we have to make all resistors to be positive. And for the voltages that are passed by the loops, there are two signs shown, so you have to get the first sign. You may wonder why I solve that way.Iit is because I want to lessen the negative signs so that I may not be confused in distributing signs.

Remember again that we have to consider that there are some elements that contain two meshes but we don't need to explain it further for i know that you already taken circuits 1.

(See problem below to see how it works).

Example Problem:

For the circuit above our task is to get the current across the 4 Ω resistor.

Loop 1, loop 2 and loop 3 are what we called the meshes. We will follow this loop to get the equations from the circuit and to solve for the current which is Io = - I2 or I2 = -Io.

Negative because the direction of I2 is opposite to the direction of our Io.

We will start,

              @ Mesh 1

           

                  8 I1 + j10 I3 - j2 I1 + j2  I2 = 0

                  I1 (8+j8) + j2   I2 - j10 I3 = 0   ------> equation 1

             @ Mesh 2

             

                  -j2 I2 + j2 I1 - j2 I2 + j2 I1 + 4 I2 + 20∠90 = 0

                    I2 (j4-4) -  - j2 I1  - j2 I3  =  20∠90 ----------> equation 2

                 

             

              @ Mesh 3

                   I3  =  5∠0 A            ------------->  equation 3

             

                   They have the same direction so current is positive.

              We already have I3 so we will substitute  equation 3 to  equation 1 and  equation 2 since the two equation contain I3.

          Our new equations are:

                 I1 (8+j8) + j2   I2  = j50   ------> equation 1

                  I2 (j4-4)  - j2 I1   =  j30 ----------> equation 2

Using matrix,

              (8+j8)      j2     =  j50

               - j2       (j4-4)   =  j30 

   

            Δ =  (8+j8)(j4-4) - ( - j2)( j2)

            Δ =  - 68

The required value is the Io so we have to get the I2. we will solve only I2. We don't need I1.

            Δ2 =  (8+j8)(j30 ) - ( - j2 ) (j50)

Yields,

           Δ2 =  -340 + j240

So,

              I2 =  (Δ2 / Δ)

              I2 =  ( -340 + j240)  /   (- 68)

              

              I2 =   6.12∠-35.22

                       Io =   6.12∠-35.22



              I've learned that In mesh analysis, from previous discussion, its basis is still the Kirchhoff's Voltage Law but the current, voltages and impedance are expressed in complex numbers and the voltage source and current source is expressed in phasor or time domain.

            As I have said from nodal analysis, in solving mesh analysis, it has the same steps in solving circuits. The only difference is it gets more complicated because there are sometimes you will confused yourself because it makes longer equation to write, additional variables and has two terms that is assigned in one element. In super mesh has the same step from previous discussion of mesh analysis we only need patience and apply the basic to more complicated problems.